暴力递归-dfs&回溯
概念
刚开始学习算法的时候,看了某大佬讲解回溯算法和 dfs 的区别:
// DFS 算法把「做选择」「撤销选择」的逻辑放在 for 循环外面
var dfs = function (root) {
if (root == null) return
// 做选择
console.log('我已经进入节点 ' + root + ' 啦')
for (var i in root.children) {
dfs(root.children[i])
}
// 撤销选择
console.log('我将要离开节点 ' + root + ' 啦')
}
// 回溯算法把「做选择」「撤销选择」的逻辑放在 for 循环里面
var backtrack = function (root) {
if (root == null) return
for (var i in root.children) {
// 做选择
console.log('我站在节点 ' + root + ' 到节点 ' + root.children[i] + ' 的树枝上')
backtrack(root.children[i])
// 撤销选择
console.log('我将要离开节点 ' + root.children[i] + ' 到节点 ' + root + ' 的树枝上')
}
}后面在 B 站看了左神的算法课,他说了这么一句话:国外根本就不存在什么回溯的概念,就是暴力递归。
纸上得来终觉浅,绝知此事要躬行!
/** 就用最简单的二叉树来看看,到底,在外面和在里面做选择与撤销选择有什么区别 */
class Node {
constructor(val) {
this.left = null
this.right = null
this.val = val
}
}
/* 构建出简单的一棵树,构建过程简单,就不赘述了
1
/ \
2 3
/ \ / \
4 5 6 7
*/
function dfs(root) {
if (root === null) return
console.log(`--->> 入 ${root.val} ---`)
for (const branch of [root.left, root.right]) {
dfs(branch)
}
console.log(`<<--- 出 ${root.val} ---`)
}
dfs(root)
console.log('🔥🔥🔥 --------------------------- 🔥🔥🔥')
function backtrack(root) {
if (root === null || root.left === null || root.right === null) return
for (const branch of [root.left, root.right]) {
console.log(`--->> ${root.val} - ${branch.val} 的树枝上; branch.val: ${branch.val}`)
backtrack(branch)
console.log(`<<--- ${root.val} - ${branch.val} 的树枝上; branch.val: ${branch.val}`)
}
}
backtrack(root)
// --->> 入 1 ---
// --->> 入 2 ---
// --->> 入 4 ---
// <<--- 出 4 ---
// --->> 入 5 ---
// <<--- 出 5 ---
// <<--- 出 2 ---
// --->> 入 3 ---
// --->> 入 6 ---
// <<--- 出 6 ---
// --->> 入 7 ---
// <<--- 出 7 ---
// <<--- 出 3 ---
// <<--- 出 1 ---
//
// 🔥🔥🔥 --------------------------- 🔥🔥🔥
//
// --->> 1 - 2 的树枝上; branch.val: 2
// --->> 2 - 4 的树枝上; branch.val: 4
// <<--- 2 - 4 的树枝上; branch.val: 4
// --->> 2 - 5 的树枝上; branch.val: 5
// <<--- 2 - 5 的树枝上; branch.val: 5
// <<--- 1 - 2 的树枝上; branch.val: 2
// --->> 1 - 3 的树枝上; branch.val: 3
// --->> 3 - 6 的树枝上; branch.val: 6
// <<--- 3 - 6 的树枝上; branch.val: 6
// --->> 3 - 7 的树枝上; branch.val: 7
// <<--- 3 - 7 的树枝上; branch.val: 7
// <<--- 1 - 3 的树枝上; branch.val: 3
观察不难发现,dfs 的 root.val 打印和 backtrack 的 branch.val 打印只是相差了第一个节点的值,这是因为回溯内做选择是直接从 「邻居」开始!
因此,“for 外选择是节点,for 内选择是树枝” — 是前人总结出来的经验,从而抽象出来的概念。学习一定要知其然且知其所以然,不能迷失在各种概念里!
总结:
-
回溯也是 dfs,只不过是特殊的策略罢了,比如「排列组合」类问题,往往都是往一个「空盒子」里装选择的节点,当空盒子满足 target 时,就是一个可行解。因为是从一个「空盒子」开始,所以也就是在各个树枝上做选择放入盒子里,因此适合在 for 内做选择。
-
传统的 dfs,就是递归穷尽到叶节点,比如求两个节点之间的距离,自然是节点与节点之间的关系,所以适合在 for 外做选择。
回溯练习-排列组合
lc.39 组合总和
/**
* @param {number[]} candidates
* @param {number} target
* @return {number[][]}
*/
var combinationSum = function (candidates, target) {
/**
* 无重复元素,所以不用剪枝
* 可以被重复选取,那么就是类似这么个树
* 1 2 3
* 1 2 3 1 2 3 1 2 3
* ..... ..... ....
*/
const res = []
const track = []
let sum = 0
/**
* 仍然不要忘记定义递归
* 输入:层级 level,输出 void; 在递归过程中把可行解塞入 res
* 结束条件,这道题比较明显 sum === target
*/
const backtrack = level => {
if (sum === target) {
res.push([...track]) // 注意拷贝一下
return
}
if (sum > target) return // 结束条件不要忘了~
// level 在这里的含义是1.在 level 层, 2.在候选数据 [level...end] 区间内做选择,通过保证元素的相对顺序,来避免重复的组合
// 如果每次都从 0 开始,那么 可能会产生 [1,2] [2,1] 这样重复的组合,不过这对排列来说,是有用的
for (let i = level; i < candidates.length; ++i) {
track.push(candidates[i])
sum += candidates[i]
backtrack(i) // 可重复使用,i + 1 则是在下一层排除了自己
track.pop()
sum -= candidates[i]
}
}
backtrack(0)
return res
}此题完全弄懂之后,排列组合就都是纸老虎了。
lc.40 组合总和 II
/**
* 与 lc.39 唯二不同,1.有重复元素,2.不能复用元素
* @param {number[]} candidates
* @param {number} target
* @return {number[][]}
*/
var combinationSum2 = function (candidates, target) {
const res = []
const track = []
let sum = 0
candidates.sort((a, b) => a - b)
const backtrack = level => {
if (sum === target) {
res.push([...track])
return
}
if (sum > target) return
for (let i = level; i < candidates.length; ++i) {
// 因为元素有重复的,所以需要先进行 「排序」,然后进行剪枝
if (i > level && candidates[i] === candidates[i - 1]) continue
track.push(candidates[i])
sum += candidates[i]
backtrack(i + 1) // 不能复用元素,下一层 level 不能包扩 i 自身
sum -= candidates[i]
track.pop()
}
}
backtrack(0)
return res
}lc.216 组合总和 III
/**
* @param {number} k
* @param {number} n
* @return {number[][]}
*/
var combinationSum3 = function (k, n) {
const res = []
const track = []
let sum = 0
const backtrack = level => {
if (sum === n && track.length === k) {
res.push([...track])
return
}
if (sum > n) return
for (let i = level; i < 10; ++i) {
if (track.length > k) continue
track.push(i)
sum += i
backtrack(i + 1)
track.pop()
sum -= i
}
}
backtrack(1)
return res
}lc.77 组合
/**
* @param {number} n
* @param {number} k
* @return {number[][]}
*/
var combine = function (n, k) {
const res = []
const track = []
const backtrack = level => {
if (track.length === k) {
res.push([...track])
return
}
for (let i = level; i <= n; ++i) {
track.push(i)
backtrack(i + 1)
track.pop()
}
}
backtrack(1)
return res
}索然无味的一题~
lc.78 子集
/**
* @param {number[]} nums
* @return {number[][]}
*/
var subsets = function (nums) {
// root
// 1 2 3
// 2 3 3
// 3
const res = [[]]
const track = []
const backtrack = level => {
// res.push([...track]) 在这里加入 是另一种无需 res 提前 [[]]
// 此处是在「节点」操作区
if (track.length === nums.length) return
for (let i = level; i < nums.length; ++i) {
track.push(nums[i])
// 在这里加入 需要 res 需要提前加一个空 []
// 此处是 「树枝」操作区
res.push([...track])
backtrack(i + 1)
track.pop()
}
}
backtrack(0)
return res
}lc.90 子集 II
/**
* @param {number[]} nums
* @return {number[][]}
*/
var subsetsWithDup = function (nums) {
const res = []
const track = []
nums.sort((a, b) => a - b)
const backtrack = level => {
res.push([...track])
if (level === nums.length) return
for (let i = level; i < nums.length; ++i) {
if (i > level && nums[i] === nums[i - 1]) continue
track.push(nums[i])
backtrack(i + 1)
track.pop()
}
}
backtrack(0)
return res
}lc.46 全排列
排列和组合最大的区别是:
- 组合无序,[1,2]和 [2,1] 是同一个组合,所以需要 level 来控制
- 排序有序,所以每次都是从 level-0 开始,但是不能重复使用元素,就需要一个 「used」(可以为一个简单的 boolean[]数组,也可以为一个栈) 来进行剪枝操作
/**
* @param {number[]} nums
* @return {number[][]}
*/
var permute = function (nums) {
const res = []
const track = []
const used = []
const backtrack = () => {
if (track.length === nums.length) {
res.push([...track])
return
}
for (let i = 0; i < nums.length; ++i) {
if (used[i]) continue // 剪枝
track.push(nums[i])
used[i] = true
backtrack()
track.pop()
used[i] = false
}
}
backtrack()
return res
}lc.47 全排列 II
/**
* @param {number[]} nums
* @return {number[][]}
*/
var permuteUnique = function (nums) {
const res = []
const track = []
const used = []
nums.sort((a, b) => a - b)
const backtrack = () => {
if (track.length === nums.length) {
res.push([...track])
return
}
for (let i = 0; i < nums.length; ++i) {
if (used[i]) continue // 去除自身剪枝
if (i > 0 && nums[i] === nums[i - 1] && !used[i - 1]) continue // 关键
track.push(nums[i])
used[i] = true
backtrack()
track.pop()
used[i] = false
}
}
backtrack()
return res
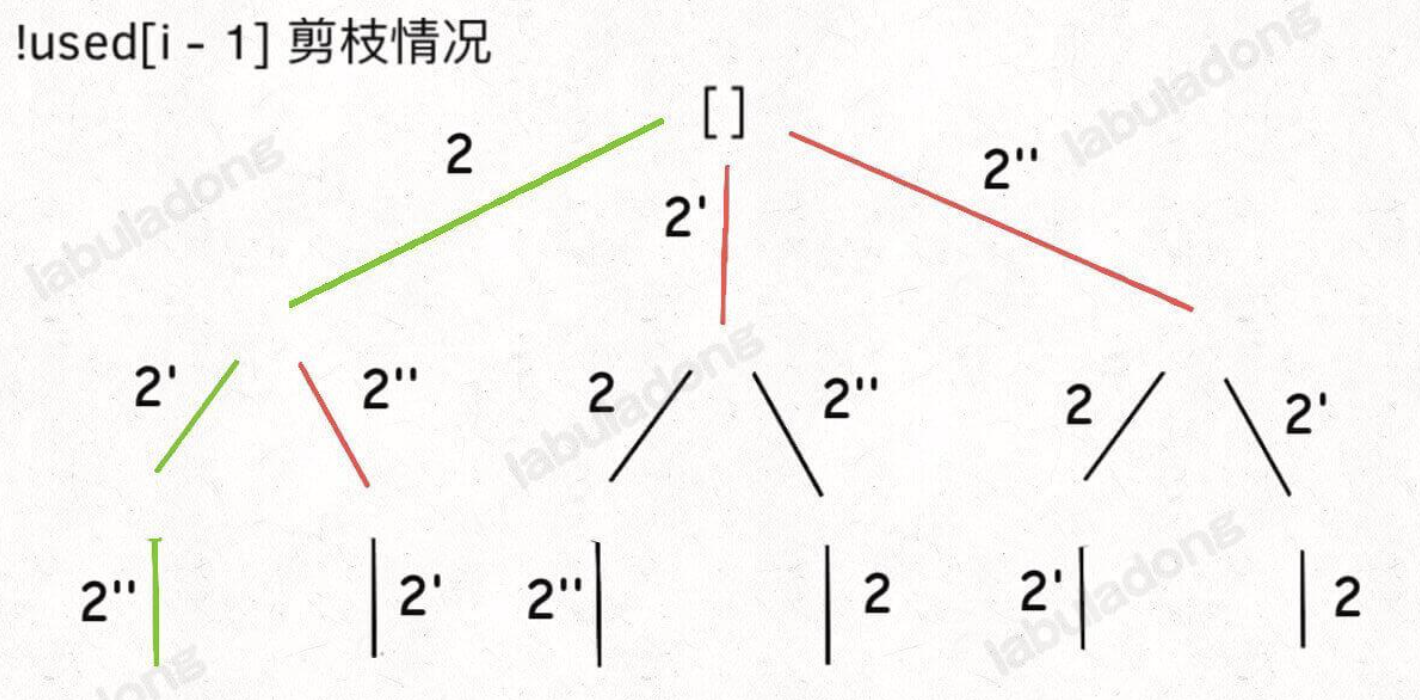
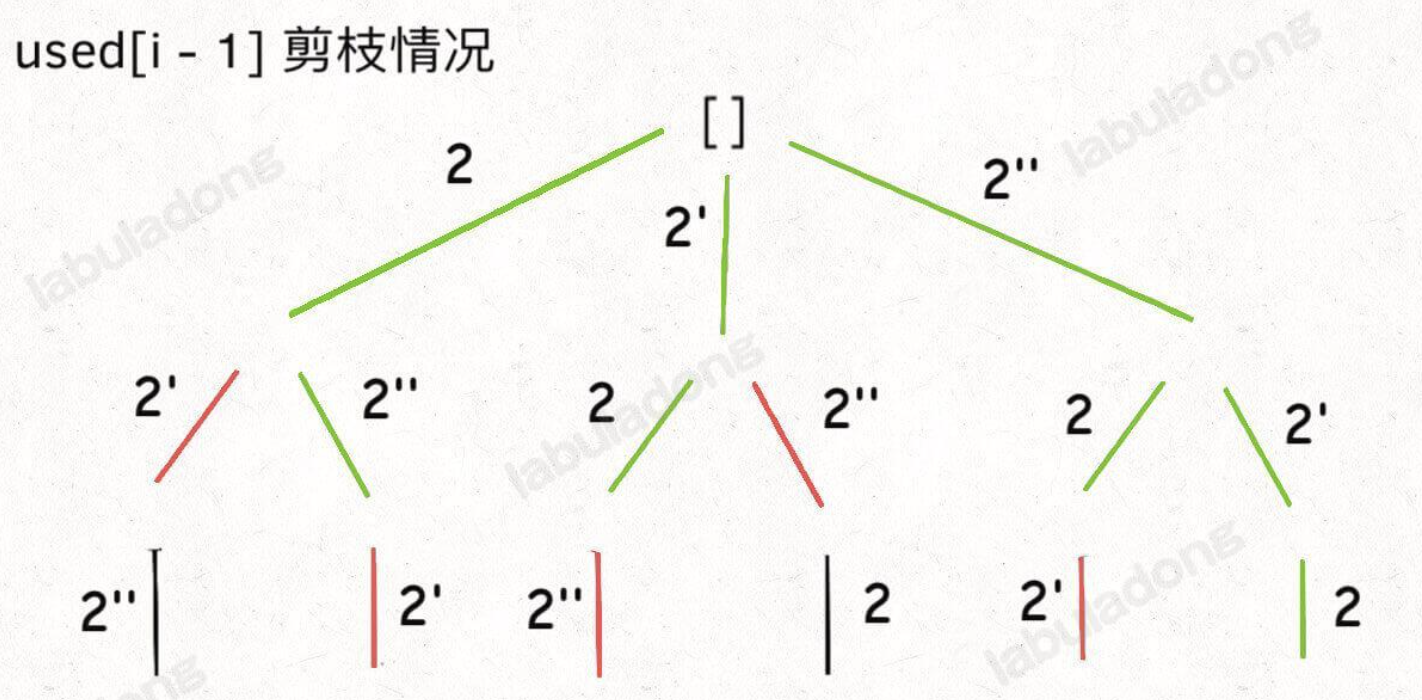
}上方 !used[i-1] 是为了去除重复的排列,当同一层前后两个元素相同时,如果前一个元素没有使用,那么就 continue,这样做的结果就是会让 [2,2',2''] 这样的数组保持固定的顺序,即 2 一定在 2’ 前,2’ 一定在 2’’ 前。如果改为 used[i-1] 也能得到去重的效果,就是固定顺序为 2’’ -> 2’ -> 2,但是剪枝的效率会大大折扣,可以参考 labuladong 大佬的示意图理解。
经典题
lc.51 N 皇后
/**
* @param {number} n
* @return {string[][]}
*/
var solveNQueens = function (n) {
// 这道题是二维的 track,所以得先初始化一个二维棋盘再说
// 同时类似组合,需要 level 来控制深度;又似排列,需要每次都遍历每一行的每一个
const res = []
const board = Array.from(Array(n), () => Array(n).fill('.'))
const backtrack = level => {
if (level === n) {
res.push([...board.map(item => item.join(''))])
return
}
for (let i = 0; i < n; ++i) {
//剪枝操作
if (!isValid(board, level, i)) continue
board[level][i] = 'Q'
backtrack(level + 1)
board[level][i] = '.'
}
}
backtrack(0)
return res
}
/**
* 判断是否合格,因为是从上往下铺的,所以只判断左上,上,右上即可
*/
function isValid(board, row, col) {
for (let i = 0; i < row; ++i) {
if (board[i][col] === 'Q') return false
}
for (let i = row - 1, j = col - 1; i >= 0; --i, --j) {
if (board[i][j] === 'Q') return false
}
for (let i = row - 1, j = col + 1; i >= 0; --i, ++j) {
if (board[i][j] === 'Q') return false
}
return true
}lc.698 划分为 k 个相等的子集
给你输入一个数组 nums 和一个正整数 k,请你判断 nums 是否能够被平分为元素和相同的 k 个子集。
典中典,也是深入理解回溯的绝佳好题,必会必懂。
// lc.416 分割两个等和子集,可以用动态规划去做,本文是 k 个子集,得上 dfs
// lc.78 是求出所有子集,这道题是固定了子集的数量,去分配
/**
* @param {number[]} nums
* @param {number} k
* @return {boolean}
*/
var canPartitionKSubsets = function (nums, k) {
if (k > nums.length) return false
const sum = nums.reduce((a, b) => a + b)
if (sum % k !== 0) return false
const bucketTarget = sum / k
const used = []
// 定义递归:输入 k 号桶, 每个数字不能重复使用,所以从 level 层开始选择
// 输出:k 号桶,是否应该把 nums[level] 加入进来
const backtrack = (k, level, bucketSum) => {
if (k === 0) return true // 所有桶装满了
// 一个桶装满了,继续下一个桶
if (bucketSum === bucketTarget) {
return backtrack(k - 1, 0, 0) // 从 0 层 0 sum 重新开始累加和
}
for (let i = level; i < nums.length; ++i) {
if (used[i]) continue // 剪枝,被用过啦
if (nums[i] + bucketSum > bucketTarget) continue // 这个数装不得,装了就超载~
used[i] = true
bucketSum += nums[i]
if (backtrack(k, level + 1, bucketSum)) return true // 递归下一个数字是否加入桶
used[i] = false
bucketSum -= nums[i]
}
return false
}
return backtrack(k, 0, 0)
}
/**
* 上方代码,逻辑上是没有问题的,但是效率低下,跑力扣的测试用例会超时
*
* 优化自然是可以想到 memo 缓存,再就是我没想到的 used 改为位运算[捂脸]。。。
*/
var canPartitionKSubsets = function (nums, k) {
if (k > nums.length) return false
const sum = nums.reduce((a, b) => a + b)
if (sum % k !== 0) return false
const bucketTarget = sum / k
let used = 0 // 使用位图技巧
const backtrack = (k, level, bucketSum, memo) => {
if (k === 0) return true
if (bucketSum === bucketTarget) {
const nextBucket = backtrack(k - 1, 0, 0, memo)
memo.set(used, nextBucket)
return nextBucket
}
if (memo.has(used)) {
// 避免冗余计算
return memo.get(used)
}
for (let i = level; i < nums.length; ++i) {
// 判断第 i 位是否是 1
if (((used >> i) & 1) === 1) {
continue // nums[i] 已经被装入别的桶中
}
if (nums[i] + bucketSum > bucketTarget) continue
used |= 1 << i // 将第 i 位置为 1
bucketSum += nums[i]
if (backtrack(k, level + 1, bucketSum, memo)) return true
used ^= 1 << i // 使用异或运算将第 i 位恢复 0
bucketSum -= nums[i]
}
return false
}
return backtrack(k, 0, 0, new Map())
}这道题,我是觉得挺有难度的。。。位运算俺着实没想到啊 😭
推荐阅读:「labuladong 球盒模型」
lc.22 括号生成
/**
* @param {number} n
* @return {string[]}
*/
var generateParenthesis = function (n) {
// 当出现右括号数量 > 左括号数量时,无效
const res = []
const track = []
const backtrack = (l, r) => {
if (l > r) return
if (l < 0 || r < 0) return
if (l === 0 && r === 0) {
res.push([...track].join(''))
return
}
/** 之前可选择的是很多个,这里就两个直接摊开写方便 */
track.push('(')
backtrack(l - 1, r)
track.pop()
track.push(')')
backtrack(l, r - 1)
track.pop()
}
backtrack(n, n)
return res
}lc.37 解数独 hard
建议先做岛屿类问题,再做此题。
/**
* 根据题意,一开始很容易写出这样子的代码,但是此刻 dfs 是什么意思呢?应该是一个探测的过程
* 也就是说 -- 此处有回溯!与岛屿类问题 flood fill 算法不同的是:flood fill 它直接就 flush 掉了找到的陆地
* 而此处的 dfs 是在不断探测的,是要走回头路的,所以这两个 for 循环是在 dfs 之内的,即:
* dfs() {for(for(选择 dfs 撤销选择))}
*/
var solveSudoku = function (board) {
for (let i = 0; i < m; ++i) {
for (let j = 0; j < n; ++j) {
if (board[i][j] === '.') {
for (let k = 1; k <= 9; ++k) {
dfs(grid, i, j, k.toString())
}
}
}
}
}
/** 开奖 */
/**
* @param {character[][]} board
* @return {void} Do not return anything, modify board in-place instead.
*/
var solveSudoku = function (board) {
dfs(board)
}
function dfs(grid) {
for (let i = 0; i < 9; ++i) {
for (let j = 0; j < 9; ++j) {
if (grid[i][j] === '.') {
for (let k = 1; k <= 9; ++k) {
// 重点是剪枝
if (!isValid(grid, i, j, k.toString())) continue
grid[i][j] = k.toString()
if (dfs(grid)) return true // 找到一种可行解 直接结束
grid[i][j] = '.'
}
return false // 9 个数字都不行
}
}
}
return true // 遍历完没有返回 false,说明找到了一组合适棋盘位置了
}
function isValid(grid, row, col, tryVal) {
for (let i = 0; i < 9; ++i) {
if (grid[row][i] === tryVal) return false
if (grid[i][col] === tryVal) return false
}
const startRow = Math.floor(row / 3) * 3
const startCol = Math.floor(col / 3) * 3
for (let i = startRow; i < startRow + 3; ++i) {
for (let j = startCol; j < startCol + 3; ++j) {
if (grid[i][j] === tryVal) return false
}
}
return true
}lc.200 岛屿的数量
首先考验的是 dfs 遍历二维数组的能力。
/**
* 在二维矩阵中的 dfs --- for{for{dfs}}
*/
function dfs(matrix, i, j, visited) {
if (i < 0 || j < 0 || i >= m || j >= n) return
/** 进节点 */
if (visited[i][j]) return
visited[i][j] = true
/** 上下左右遍历 */
dfs(matrix, i - 1, j)
dfs(matrix, i + 1, j)
dfs(matrix, i, j - 1)
dfs(matrix, i, j + 1)
/** 出节点 */
}
/** 此外有方向数组的技巧 */
const dirs = [
[-1, 0],
[1, 0],
[0, -1],
[0, 1]
]
// 把上方的四个 dfs 配合 dirs 改为 for 循环即可
for (var d of dirs) {
const next_i = i + d[0]
const next_j = j + d[1]
dfs(matrix, next_i, next_j, visited)
}/**
* @param {character[][]} grid
* @return {number}
*/
var numIslands = function (grid) {
let res = 0
const m = grid.length
const n = grid[0].length
const visited = Array.from(Array(m), () => Array(n).fill(false))
for (let i = 0; i < m; ++i) {
for (let j = 0; j < n; ++j) {
// 从某个陆地节点开始 detect
if (grid[i][j] === '1') {
res++
dfs(grid, i, j, visited)
}
}
}
return res
}
function dfs(grid, i, j, visited) {
const m = grid.length
const n = grid[0].length
if (i < 0 || j < 0 || i >= m || j >= n) return
if (grid[i][j] === '0') return
grid[i][j] = '0' // 淹没土地
dfs(grid, i - 1, j, visited)
dfs(grid, i + 1, j, visited)
dfs(grid, i, j - 1, visited)
dfs(grid, i, j + 1, visited)
}这种“淹掉岛屿”的 dfs 算法有自己的名字 — 「经典的 Flood fill 算法」,这样可以不用维护 visited 数组。如果题目要求不能修改原数组,那么还是用 visited 去做,就此题而言具体就是多两步操作,一个是在 res++ 前判断是否 visit 过,另一个就是在每次 dfs 前判断是否 visit 过。
另外此题还可以使用 BFS 和 并查集 解决
lc.695 岛屿的最大面积
/**
* @param {number[][]} grid
* @return {number}
*/
var maxAreaOfIsland = function (grid) {
let maxArea = 0
const m = grid.length
const n = grid[0].length
for (let i = 0; i < m; ++i) {
for (let j = 0; j < n; ++j) {
if (grid[i][j] === 1) {
maxArea = Math.max(maxArea, dfs(grid, i, j))
}
}
}
return maxArea
}
// 继续 flood fill
function dfs(grid, i, j) {
const m = grid.length
const n = grid[0].length
if (i < 0 || j < 0 || i >= m || j >= n) return 0
if (grid[i][j] === 0) return 0
grid[i][j] = 0
return dfs(grid, i - 1, j) + dfs(grid, i + 1, j) + dfs(grid, i, j - 1) + dfs(grid, i, j + 1) + 1
}lc.1020 飞地的数量
/**
* @param {number[][]} grid
* @return {number}
*/
var numEnclaves = function (grid) {
let res = 0
const m = grid.length
const n = grid[0].length
// 先把四个边界的淹没掉
for (let i = 0; i < m; ++i) {
dfs(grid, i, 0)
dfs(grid, i, n - 1)
}
for (let i = 0; i < n; ++i) {
dfs(grid, 0, i)
dfs(grid, m - 1, i)
}
for (let i = 0; i < m; ++i) {
for (let j = 0; j < n; ++j) {
if (grid[i][j] === 1) {
res++
}
}
}
return res
}
function dfs(grid, i, j) {
const m = grid.length
const n = grid[0].length
if (i < 0 || j < 0 || i >= m || j >= n) return
if (grid[i][j] === 0) return
grid[i][j] = 0
dfs(grid, i - 1, j)
dfs(grid, i + 1, j)
dfs(grid, i, j - 1)
dfs(grid, i, j + 1)
}lc.1254 统计封闭岛屿的数目
/**
* @param {number[][]} grid
* @return {number}
*/
var closedIsland = function (grid) {
let res = 0
const m = grid.length
const n = grid[0].length
for (let i = 0; i < m; ++i) {
dfs(grid, i, 0)
dfs(grid, i, n - 1)
}
for (let j = 0; j < n; ++j) {
dfs(grid, 0, j)
dfs(grid, m - 1, j)
}
for (let i = 0; i < m; ++i) {
for (let j = 0; j < n; ++j) {
if (grid[i][j] === 0) {
res++
dfs(grid, i, j)
}
}
}
return res
}
function dfs(grid, i, j) {
const m = grid.length
const n = grid[0].length
if (i < 0 || j < 0 || i >= m || j >= n) return
if (grid[i][j] === 1) return
grid[i][j] = 1
dfs(grid, i - 1, j)
dfs(grid, i + 1, j)
dfs(grid, i, j - 1)
dfs(grid, i, j + 1)
}lc.1905 统计子岛屿
这道题需要稍微思考一下,同样大小的 grid,统计 grid2 中的子岛屿,直接遍历是不太好操作的,得先排除掉非子岛屿,然后再统计。什么是非子岛屿,那就是在 grid 中是陆地,但是在 grid1 中是海洋,直接淹掉,这样最后再遍历的时候剩下的就都是子岛屿啦。
/**
* @param {number[][]} grid1
* @param {number[][]} grid2
* @return {number}
*/
var countSubIslands = function (grid1, grid2) {
let res = 0
const m = grid2.length
const n = grid2[0].length
for (let i = 0; i < m; ++i) {
for (let j = 0; j < n; ++j) {
if (grid2[i][j] === 1 && grid2[i][j] !== grid1[i][j]) {
dfs(grid2, i, j)
}
}
}
for (let i = 0; i < m; ++i) {
for (let j = 0; j < n; ++j) {
if (grid2[i][j] === 1) {
res++
dfs(grid2, i, j)
}
}
}
return res
}
function dfs(grid, i, j) {
const m = grid.length
const n = grid[0].length
if (i < 0 || j < 0 || i >= m || j >= n) return
if (grid[i][j] === 0) return
grid[i][j] = 0
dfs(grid, i - 1, j)
dfs(grid, i + 1, j)
dfs(grid, i, j - 1)
dfs(grid, i, j + 1)
}这道题自然也是可以使用 「并查集」来解决,后序并查集章节会详细使用。
请注意,本文所有的回溯函数,都使用了闭包的特性,如果不使用闭包,把需要的参数变为回溯函数的入参即可。
我亦无他,唯手熟尔!peace~